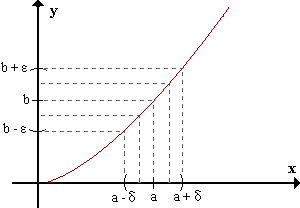
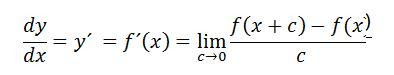DERIVADAS : La derivada es el ritmo de cambio de cualquier fricción en un punto e instante determinado, la derivada es la pendiente de la recta tangente que pasa por un punto especifico de una curva, siendo su proceso mecánico el calculo diferencial.
DERIVADAS : La derivada es el ritmo de cambio de cualquier fricción en un punto e instante determinado, la derivada es la pendiente de la recta tangente que pasa por un punto especifico de una curva, siendo su proceso mecánico el calculo diferencial.LINEAS NOTABLES DE LA CIRCUNFERENCIA:
- SECANTE: A traviesa la circunferencia.
- TANGENTE: toca un solo punto de la circunferencia.
- RADIO: Linea que va del centro de la circunferencia a otro punto.
- DIAMETRO: Pasa por el centro de la circunferencia.

En este primer video daremos a conocer como y por qué sale la ecuación de Derivación con relación a Límites que mas adelante nos permitirá entender y desarrollar ejercicios involucrados con dicho tema.
En los siguientes vídeos se exponen claros ejemplos acerca de como desarrollar un ejercicio de Derivación con respecto a Límites.
FORMULA DE DERIVADA UTILIZANDO LA DEFINICIÓN DE DE LIMITES :